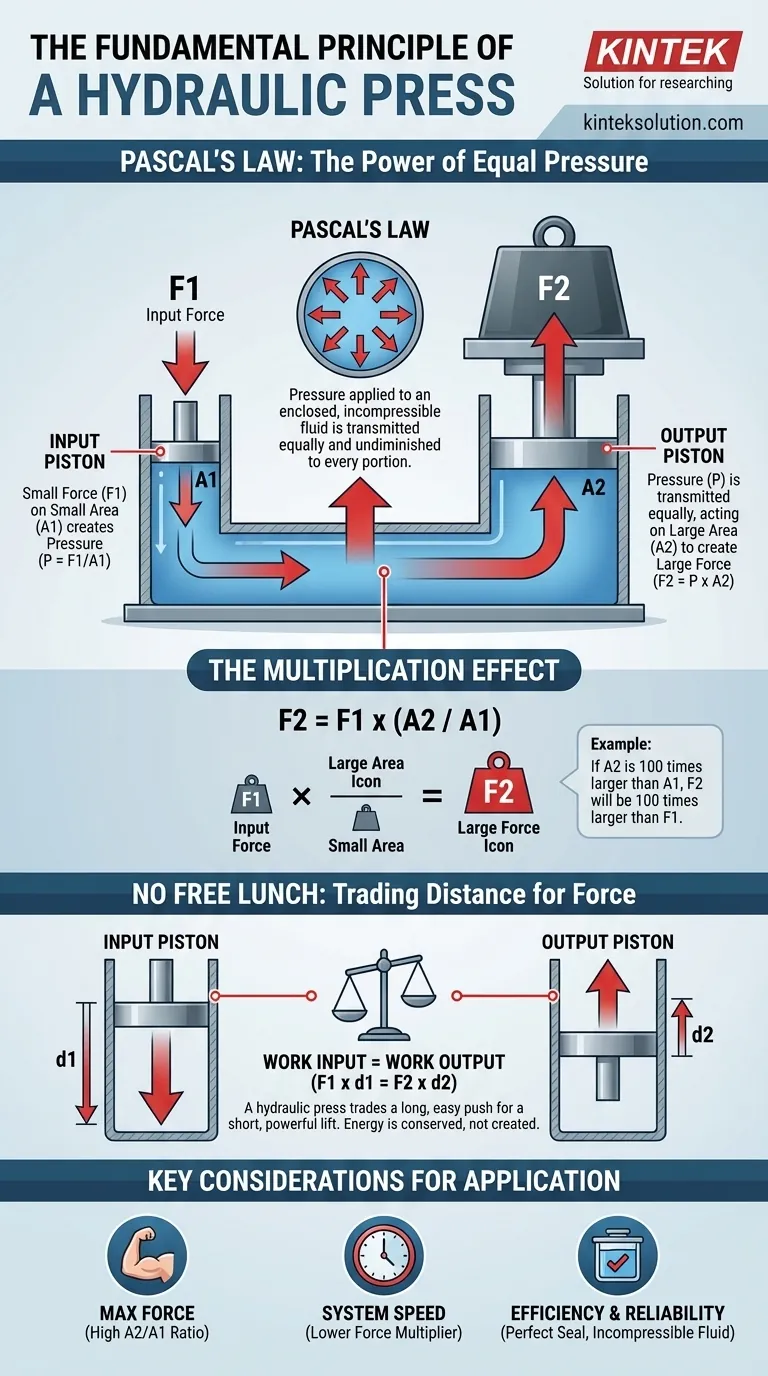
O princípio fundamental é a Lei de Pascal, que permite uma imensa multiplicação de força. Esta lei afirma que a pressão aplicada a um fluido confinado e incompressível é transmitida de forma igual e sem diminuição a cada porção do fluido e às paredes do seu recipiente. Numa prensa hidráulica, isto significa que uma pequena força aplicada a uma pequena área gera uma pressão que, ao atuar sobre uma área maior, produz uma força de saída proporcionalmente maior.
Uma prensa hidráulica não cria energia, mas sim troca distância por força. Ao aplicar uma pequena força ao longo de uma grande distância num pistão pequeno, gera-se uma força imensa que move uma distância muito curta num pistão grande, tudo graças à pressão uniforme do fluido confinado.
Desvendando a Lei de Pascal
O funcionamento de uma prensa hidráulica parece quase mágico, mas depende de três conceitos distintos que trabalham em uníssono: um fluido confinado, a definição de pressão e o princípio de transmissão igual.
O Papel do Fluido Confinado
Um sistema hidráulico é um circuito fechado, geralmente preenchido com um fluido incompressível como óleo. "Incompressível" é a propriedade chave; significa que o volume do fluido não diminui notavelmente sob pressão.
Como o fluido não pode ser espremido num espaço menor, qualquer força aplicada a ele é imediatamente convertida em pressão que procura atuar sobre todo o recipiente.
Pressão: O Grande Equalizador
A pressão é definida como Força dividida pela Área (P = F/A). Não é a força em si, mas a distribuição dessa força sobre uma superfície.
Imagine a diferença entre ser pisado por um sapato plano versus um salto agulha. A força (o seu peso) é a mesma, mas a minúscula área do salto agulha concentra essa força numa pressão imensa. A Lei de Pascal alavanca exatamente essa relação.
Transmissão Igual e Sem Diminuição
Este é o cerne da Lei de Pascal. Quando aplica pressão a uma parte do fluido confinado, essa exata quantidade de pressão fica instantaneamente disponível em todo o lado dentro do sistema.
Pense num saco plástico selado cheio de água. Se o perfurar com o dedo num ponto, o saco inteiro fica esticado. A pressão que aplicou não é sentida apenas debaixo do seu dedo; é transmitida igualmente a todas as superfícies internas do saco.
A Mecânica da Multiplicação de Força
A genialidade da prensa hidráulica reside no seu uso de dois pistões com áreas de superfície diferentes para explorar a Lei de Pascal e criar uma vantagem mecânica.
O Pistão de Entrada (Pequena Força, Pequena Área)
O processo começa no pistão menor, frequentemente chamado de pistão de esforço. Uma modesta força de entrada (F1) é aplicada à sua pequena área de superfície (A1).
Esta ação gera uma pressão específica no fluido: P = F1 / A1.
O Pistão de Saída (Grande Força, Grande Área)
Esta pressão é transmitida, sem diminuição, por todo o fluido. Ela agora empurra contra a parte inferior do pistão de saída muito maior, que tem uma área de superfície de A2.
Como a pressão é a mesma em todo o lado, a força exercida no pistão de saída (F2) é igual a essa pressão multiplicada pela área maior: F2 = P x A2.
O Efeito de Multiplicação
Ao substituir a primeira equação na segunda, obtemos a relação: F2 = (F1 / A1) x A2.
Isto pode ser simplificado para F2 = F1 x (A2 / A1). O termo (A2 / A1) é o fator de multiplicação de força. Se o pistão de saída tiver 100 vezes a área de superfície do pistão de entrada, a força de saída será 100 vezes a força de entrada.
Compreendendo as Trocas: Não Há Almoço Grátis
A enorme amplificação de força de uma prensa hidráulica pode parecer violar as leis da física, mas não o faz. O sistema é regido pela conservação de energia.
A Lei da Conservação de Energia
Uma prensa hidráulica não pode criar mais energia do que a que lhe é fornecida. É um multiplicador de força, não um multiplicador de energia.
A Relação Trabalho-Distância
O trabalho é definido como Força multiplicada pela Distância (W = F x d). Ignorando perdas mínimas devido ao atrito, o trabalho realizado no pistão de entrada deve ser igual ao trabalho realizado pelo pistão de saída.
Portanto, F1 x d1 = F2 x d2.
Trocar Distância por Força
Como sabemos que a força de saída (F2) é muito maior do que a força de entrada (F1), a distância de saída (d2) deve ser proporcionalmente menor do que a distância de entrada (d1).
Para levantar um carro pesado uma polegada usando o pistão grande, pode ter que empurrar o pistão pequeno para baixo vários pés. Está a trocar um empurrão longo e fácil por um levantamento curto e poderoso.
Fazendo a Escolha Certa para a Sua Aplicação
Aplicar este princípio requer a compreensão de como a alteração de uma variável afeta as outras.
- Se o seu foco principal for a saída máxima de força: Priorize maximizar a razão de área entre os pistões de saída e de entrada (A2/A1). Uma razão maior traduz-se diretamente num fator de multiplicação de força mais elevado.
- Se o seu foco principal for a velocidade do sistema: Deve aceitar uma menor multiplicação de força. Uma razão de área menor significa que o pistão de saída viajará uma distância maior para cada curso do pistão de entrada.
- Se o seu foco principal for a eficiência e a fiabilidade: Garanta que o sistema esteja perfeitamente selado para evitar fugas de fluido, que causam perda de pressão. Use um fluido hidráulico incompressível de alta qualidade para garantir que a força de entrada seja traduzida diretamente em pressão.
Em última análise, projetar ou usar um sistema hidráulico é um exercício de equilibrar esta troca fundamental entre força e distância para atingir o seu objetivo específico.
Tabela de Resumo:
| Conceito | Ideia Chave | Aplicação na Prensa Hidráulica |
|---|---|---|
| Lei de Pascal | A pressão num fluido confinado é transmitida de forma igual e sem diminuição | Permite a multiplicação de força através das razões de área do pistão |
| Multiplicação de Força | Força de saída = Força de entrada × (Razão de área) | Atinge forças elevadas para tarefas como testes de materiais em laboratórios |
| Conservação de Energia | Trabalho de entrada iguala o trabalho de saída (F1 × d1 = F2 × d2) | Garante a ausência de criação de energia, apenas troca de força-distância |
| Propriedades do Fluido | Fluidos incompressíveis como o óleo mantêm a integridade da pressão | Crítico para uma operação fiável em ambientes laboratoriais |
Pronto para melhorar as capacidades do seu laboratório com prensas hidráulicas fiáveis? A KINTEK é especializada em máquinas de prensa de laboratório, incluindo prensas de laboratório automáticas, prensas isostáticas e prensas de laboratório aquecidas, concebidas para fornecer controlo de força preciso e eficiência para as suas necessidades de pesquisa e teste. O nosso equipamento alavanca princípios como a Lei de Pascal para garantir um desempenho ideal, ajudando-o a alcançar resultados precisos na compressão de materiais, moldagem e muito mais. Contacte-nos hoje para discutir como as nossas soluções podem apoiar as suas aplicações específicas e aumentar a produtividade do seu laboratório!
Guia Visual
Produtos relacionados
- Prensa hidráulica de laboratório Prensa de pellets de laboratório 2T para KBR FTIR
- Prensa hidráulica automática para laboratório Máquina de prensagem de pellets para laboratório
- Prensa hidráulica de laboratório Prensa de pellets de laboratório Prensa de bateria de botão
- Prensa hidráulica automática de laboratório para prensagem de pellets XRF e KBR
- Prensa hidráulica de laboratório manual Prensa de pellets de laboratório
As pessoas também perguntam
- Quais são as vantagens de utilizar a prensa hidráulica portátil para fabricar pastilhas de KBr?Obter uma preparação de amostras FT-IR superior
- Como é que uma prensa hidráulica é utilizada na preparação de amostras para espetroscopia?Obter Pellets de Amostra Precisos e Homogéneos
- Quais são algumas das aplicações laboratoriais das prensas hidráulicas?Aumentar a precisão na preparação e ensaio de amostras
- Como as prensas hidráulicas são usadas na espectroscopia e determinação composicional? Aumentando a precisão na análise FTIR e XRF
- Como é que as prensas hidráulicas garantem a precisão e a consistência na aplicação da pressão?Explicação das principais caraterísticas
